[最も共有された！ √] y=x^2 2x-8 in vertex form 304863

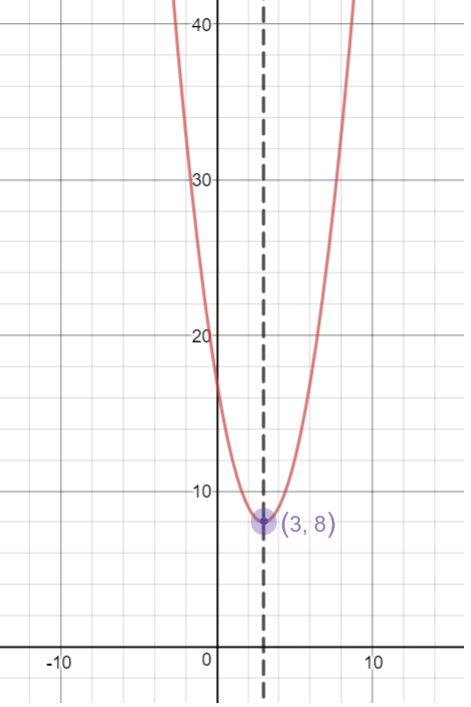
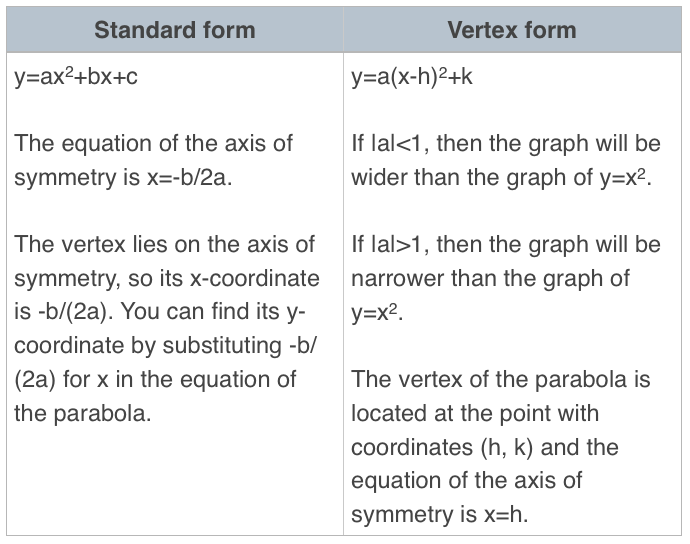
 Suppose a parabola has a vertex (4,7) and also passes through the point (3,8) Write the equation of the parabola in vertex form f(x)=a(xh)^2k I believe h=4 k=7 Not sure what to do from here MathFrom this chart, we see that the parabola y = x 2 contains the points (3, 9) and (4, 16) On the other hand, he parabola y = 2x 2 contains the points (3, 18) and (4, 32) On the first equation, y = x 2, to move horizontally across the xaxis from x = 3 to x = 4, we move up vertically on the yaxis from y = 9 to y = 16 which is 7 unitsSo, to go from the point (3, 9) to (4, 16), we move over 1See the answer See the answer See the answer done loading

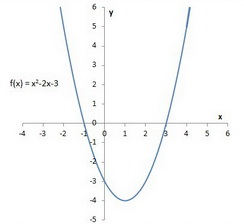
How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic

Y=x^2 2x-8 in vertex form

Y=x^2 2x-8 in vertex form-Y = x2 − 2x − 8 y = x 2 2 x 8 Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 8 x 2 2 x 8 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = − 8 a = 1, b = 2, c = 8 Consider the vertex form of a parabolaTo find the vertex form of the parabola, we use the concept completing the square method Vertex form of a quadratic function y = a(x h) 2 k In order to find the maximum or minimum value of quadratic function, we have to convert the given quadratic equation in the above form

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Vertex form is y = 2 (x 6)^2 – 13 Standard form of given equation is y = 2 x^2 24 x 59 Where, Characteristic Points are Vertex P (6, 13) Yintercept P (0, 59) An online parabola vertex calculator can display a parabola graph with exact values when you substitute the same values for a vertex form equation5 hours ago Substitute (3, 8) for ( x, y) in the vertex form to find a The function of the parabola is 62/87,21 From the figure, the vertex ( h, k) of the parabola is (±3, 2) Substitute ( ±1, 8) for ( x, y) in the vertex form to find a The function of the parabola is Write each function inGive the vertex of each function, and graph it How does vertex form compare to the other forms in each problem?

10) Use your calculator to find the vertex, xintercepts, and yintercept Do they match yours?Question Write y=2x^212x14 in vertex form Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website! Explanation Changing a quadratic function from standard form to vertex form actually requires that we go through the process of completing the square To do this, we need the x2 and x terms only on the right side of the equation y = x2 2x −8 y 8 = x2 2x −8 8 y 8 = x2 2x −8 8 y 8 = x2 2x

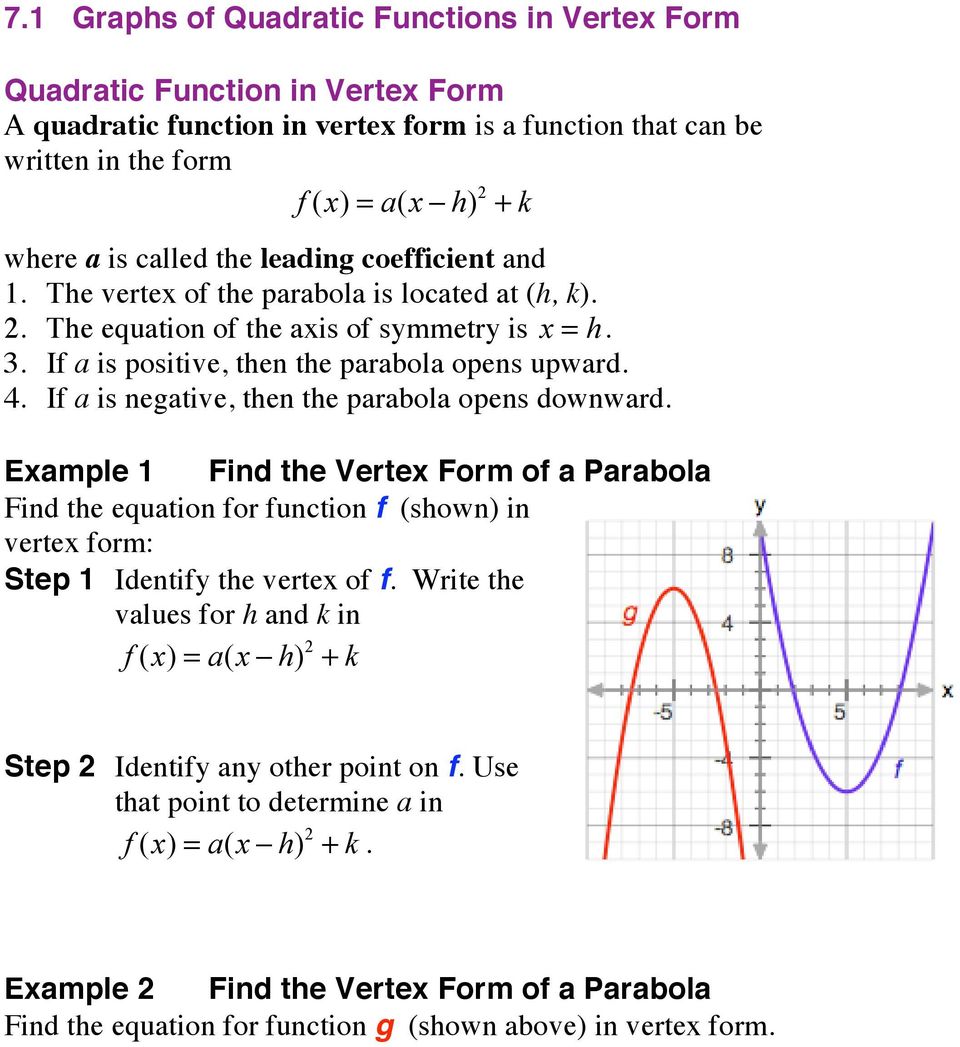
11) y = (x 3)2 2 12) y = (x 4)2 13) y = x2 3 14) y = x2 3 Convert each function to standard form Give the vertex and yinterceptThe ycoordinate of the vertex is $$ y = f(1) = 1^22\cdot12 = 1 2 2 = 1 $$ The yintercept is $$ y = f(0) = 0^22\cdot02 = 0 0 2 = 2 $$ In this case xintercept doesn't exist since equation $x^22x2=0$ does not has the solutions (use quadratic equation solver to check ) So, in this case we will plot the graph using onlySection 111 Graphs and Vertex Form In this section, we will explore quadratic functions and, in particular, their vertex and factored forms Example 1111 Maia has a remotecontrolled airplane and she is going to do a stunt dive where the plane dives

Biomath Quadratic Functions

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet

Example 13 Rewrite in y = a (x − h) 2 k form and determine the vertex y = 2 x 2 − 4 x 8 Solution Since a = 2, factor this out of the first two terms in order to complete the square Leave room inside the parentheses to add a constant termY = a (xh)^2 k is the vertex form equation Now expand the square and simplify You should get y = a (x^2 2hx h^2) k Multiply by the coefficient of a and get y = ax^2 2ahx ah^2 k This is standard form of a quadratic equation, with the normal a, b and c in ax^2 bx c equaling a, 2ah and ah^2 k, respectivelyIn this section, we will explore quadratic functions using graphing technology and learn the vertex and factored forms of a quadratic function's formula

13 The Following Quadratic Function Is Written In General Form F X X2 6x 7 A Write The Factored Form Homeworklib

Vertex Form Of Quadratic Functions Math 2 Y

Subtract 3 from both sides x^ {2}2x=y3 Multiply 2 and 1 to get 2 x^ {2}2x1=y31 Divide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}2x1=y2 AddSubtract y from both sides Subtract y from both sides x^ {2}2x1y=0 x 2 2 x 1 − y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 1y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation isOur perfect square trinomial factors into two identical binomials, (x6)•(x6) The vertex of an equation in vertex form

3 Vertex Form

Graphing Parabolas

 But the equation for a parabola can also be written in "vertex form" y = a(x ?Regents Exam Questions FIFC8 Vertex Form of a Quadratic Name _____ wwwjmaporg 1 FIFC8 Vertex Form of a Quadratic 1 In the 8 Determine and state the vertex of f(x) =x2 −2x−8 using the method of completing the square 9 Use the method of completing the square to determine the vertex of f(x) =x2 −14x−15 State y 9/8 = 2(x 2 3/2 x 9/16) y 9/8 = 2(x 3/4) 2 y = 2(x 3/4) 2 9/8 The above equation represent the standard form of the equation of parabola The standard form of the parabola with vertex (h, k) and axis of symmetry x = h is y = a(x h) 2 k The vertex form of the equation of parabola is y = 2(x 3/4) 2 9/8 and Vertex (h

Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

Biomath Quadratic Functions

To Convert from f (x) = ax 2 bx c Form to Vertex Form Method 1 Completing the Square To convert a quadratic from y = ax 2 bx c form to vertex form, y = a(x h) 2 k, you use the process of completing the square Let's see an example Convert y = 2x 2 4x 5 into vertex form, and state the vertex While the standard quadratic form is a x 2 b x c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 k In both forms, y is the y coordinate, x is the x coordinate, and a is the constant that tells you whether the36 is the value for 'c' that we found to make the right hand side a perfect square trinomial;

Transformations Of Quadratic Functions College Algebra

Vertex Form Of A Quadratic Equation Algebra Socratic

Question Rewrite the equation y=–2x^24x3 in vertex form Identify the vertex and the axis of symmetry Answer by ewatrrr(243) (Show Source) You can put this solution on YOUR website! x = b/2a = 4/4 = 1 y (1) = 4 vertex at (1 , 4) Edit or in vertex form y = 2 (x 1)^2 4 vertical shift down 4 units hope that helped acobdarfq and 8 more users found this answer helpful heart outlinedWrite the following quadratics in vertex form by completing the square and find the vertex Example 1 y = x 2 2x 4 Solution Using completing the square method, y = (x 2 2x

Marcus Needs To Rewrite F X X2 6x 4 In Vertex Form

Bingo Graphing Quadratics Parabolas In Vertex Form By Algebra Made Fun

3 must be factored from 3x2 9x x must be factored from 3x2 9x 9 must be factored from 9x 18 3 must be factored from 3x2 18 A Which phrase best describes the translation from the graph y = 6x2 to the graph of y = 6 (x 1)2?We want to put it into vertex form y=a (xh) 2 k We can convert to vertex form by completing the square on the right hand side Adding 18 to both sides gives us a perfect square trinomial on the right The vertex of a quadratic equation in vertex form is (h,k), so our vertex is (3,22)Y = 2x2 –4x –1 STEP 2 Find the vertex y x y 2 1 4 1 1 32 Thus the vertex is (1 ,–3) Since the x –value of the vertex is given by the line of symmetry, we

Fireworks From Standard To Vertex Form Ppt Video Online Download

View Question What Is The Vertex Of The Equation Y X 2 2x 8

 Methods for solving quadratic equations We find the vertex of a quadratic equation with the following steps Get the equation in the form y = ax2 bx c Calculate b / 2a This is the xcoordinate of the vertex To find the ycoordinate of the vertex, simply plug the value of b / 2a into the equation for x and solve for yY = 2 (x 9) 2 8 is the given equation in vertex form The vertex is (− 9, 8)Free functions vertex calculator find function's vertex stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy

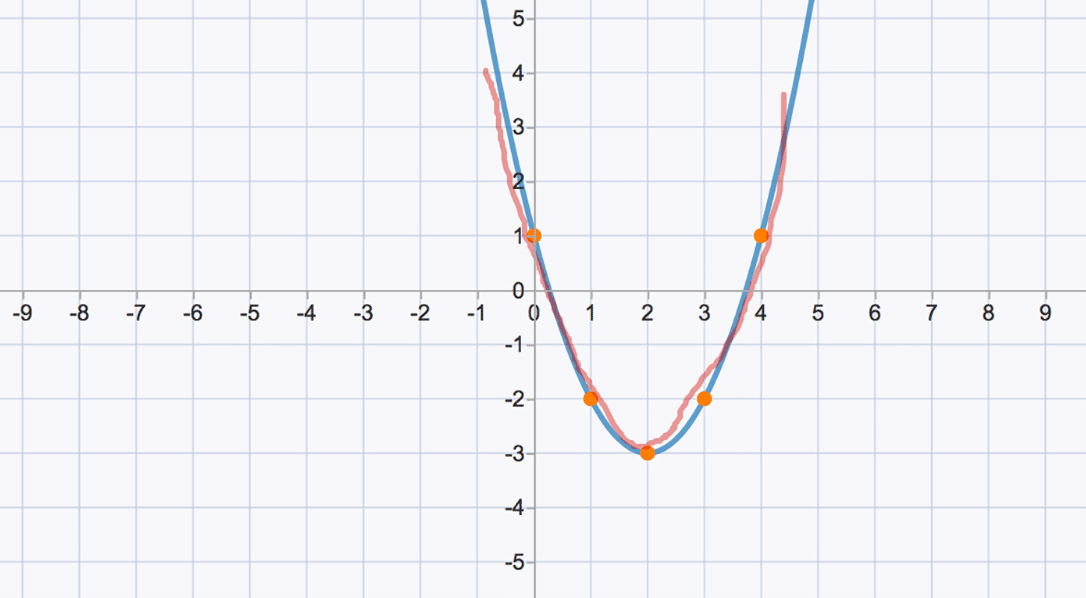
What Is Vertex Form Example Get Education

Vertex Form Vertex Form Vertex Form Is Another

Y = 3(x ) 2 y = 3(x ) 2 This is our equation in vertex form, which tells us that the vertex is at (, ), and also that our parabola opens upwards, since a (3 in this case) is positive To convert from vertex form to standard form, we simply expand vertex form We can confirm that our above equation in vertex form is the same as the original equation in standard form by expanding it yWhich equation is y=3(x2)^2(x5)^2 rewritten in vertex form?None y = 3(x 2)² (x 5)² y = 3(x 2)(x 2) (x 5)(x 5)Answer Vertex form of quadratic equation is => Y = a(X h)^2 k Let's simplify the given equation Add and subtract coefficient of X^2 on left side Y = 4X^2 8X 4 4 3 => Y = 4(X^2 2X 1) 4 3 => Y = 4(X 1)^2 1 So vertex of this parabola is V = (1,1)

How To Go From Standard Form To Vertex Form By Completing The Square

Y X

Section 132 Quadratic Graphs and Vertex Form Objectives PCC Course Content and Outcome Guide MTH 95 CCOG 5b;Answer to Solved 2) y=x2 – 2x 5 2) y=x2 2x 5 Vertex Form of This problem has been solved!How to Graph a Parabola of the Form {eq}y=x^2 bx c {/eq} Example 1 Our quadratic equation is {eq}y = x^2 2x 3 {/eq} Step 1 First we need to find the vertex of our parabola The vertex

How To Write The Equation Of The Parabola In Vertex Form Quora

Solved Use The Information Provided To Write The Vertex Form Chegg Com

The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens down The equation is y = x 2 2x 2 To change the expression (x 2 2x) into a perfect square trinomial add (half the x coefficient)² to each side of the expression Here x coefficient = 2 So, (half the x coefficient) 2 = (2/2) 2 = 1 Add and subtract 1 to the expression y = (x 2 2x 2 1 1) y = (x 2 2x 1 2 1) y = (x 2 2x 1 3) y = (x 2 2(1)(x) 1 ²) 3H)2 k Question Updated PM 1 Answer/Comment yeswey The minimum value of a parabola that opens upward will be its vertex TRUE Added PM

Solved Write X 2 4x 3 In The Form Y X H 2 K Chegg Com

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Complete the statements below that show y = 8x2 32x 17 being converted to vertex form Factor out the leading coefficient y = 8(x2 4x) 17 1 Form a perfectsquare trinomial y = 8(x2 4x ____) 17 ____ 2 Write in vertex form y = 8(x ____)2 ____6 unit left 6 unit right 1 unit left If the equation has the form y = ax 2 bx c, the xcoordinate of the vertex is x = b/(2a) For the problem y = x 2 2x 8, a = 1, b = 2, and c = 8, so, the xcoordinate of the vertex is x = 2/2 or 1 Substituting this value back into the equation y = (1) 2 2(1) 8 = 9

Solution Write Each Function In Vertex Form Sketch The Graph Of The Function And Label Its Vertex 33 Y X2 4x 7 34 Y X2 4x 1 35 Y 3x2 18x 36 Y 1 2x2 5x

What Is The Axis Of Symmetry And Vertex For The Graph F X X 2 2x 8 Socratic

C = −4 vertex f orm y = a(x−h)2 k where h = −b 2a and k = −(b2−4ac) 4a h =− −14 2⋅2 = −7 2 k = −(142−4⋅2⋅(−4)) 4⋅2 = −() 8 = −228 8 = −57 2 Answer y =2(x 7 2)2 − 57 2 y = 2 x 2 14 x − 4Start with the given quadratic Subtract from both sides Factor out the leading coefficient This step is important since we want the coefficient to be 1 Take half of the x coefficient to get (ie )We can convert to vertex form by completing the square on the right hand side;

Vertex Form Of Parabolas Kuta Software

7 1 Graphs Of Quadratic Functions In Vertex Form Quadratic Flip Ebook Pages 1 39 Anyflip Anyflip

Substitute the value of the x x coordinate in the given function vy = 2(2)2−8(2)4 v y = 2 ( 2) 2 − 8 ( 2) 4 Solving, we obtain the y y coordinate of the vertex of the parabola vy = 2(4 algebra determine the vertex for the function y=2x^25x3 for y = ax^2 bx c, the x value of the vertex is b/ (2a) sub that x into your equation to find the y Another way is to complete the square so for yours, x = 5/4 etc a third way, if you know Calculus, asked by Shay on Math The result is the same as 1 * 1, which is 1 Next, simplify 2 * 1 The result is 2 Then, add 1 and 2 The answer will be 1 Finally, add 1 and 8 to get the ycoordinate 7 The ordered pair of the vertex is (1,7) Hope this helps!

How To Graph A Quadratic Equation 10 Steps With Pictures

Converting Quadratic Equations Worksheet Coach Forrester

In comparing the graphs of y = x 2 (red), y = 2x 2 (green), and y = 4x 2 (blue), we see that each parabola opens upward but the larger the value of "a", the steeper (narrower) the graph Thus, when a ³ 1, the parabola opens upward, and as the value ofHi the vertex form of a parabola, where(h,k) is the vertexThe vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the ycoordinate This means If the vertex form is , then the vertex is at (hk) How to put

Untitled Document

Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube

We want to put it into vertex form y=a(xh) 2 k;Convert to vertex form y=2x^214x4 Convert to vertex form y=2x^214x4 y =2x2 14x −4 a =2;Graph y=x^22x8 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up

Mxcy1ggb7uzkpm

Vertex Form Of A Quadratic Equation

Following quadratic functions in the vertex form y = a(x — k Identify the turning point of the quadratic from this form State whether it is a maximum or a minimum l y=x22x 15 2 y = xž 32 3 y 6x 5 4 y = £ 8x 40 qo8\ y = 16K 130 6 75 7 lox 24 Q 8 y 32x 16 21 T I 10 y = —S ( (00 80 ll y = 4x2 56x qRegistered From Posted Saturday 30th of Dec 0933 Hi, I am a senior in high school and need major help in convert to vertex form calculator My math grades are awful and I have decided to do something about it I am looking for some software that will allow me to enter a question and gives detailed step by step solution

Solved For The Parabola Y 2x 2 8x 5 Which Of The Chegg Com

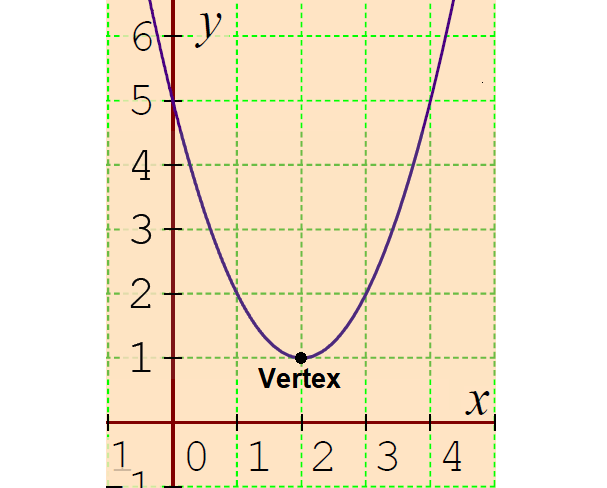
2

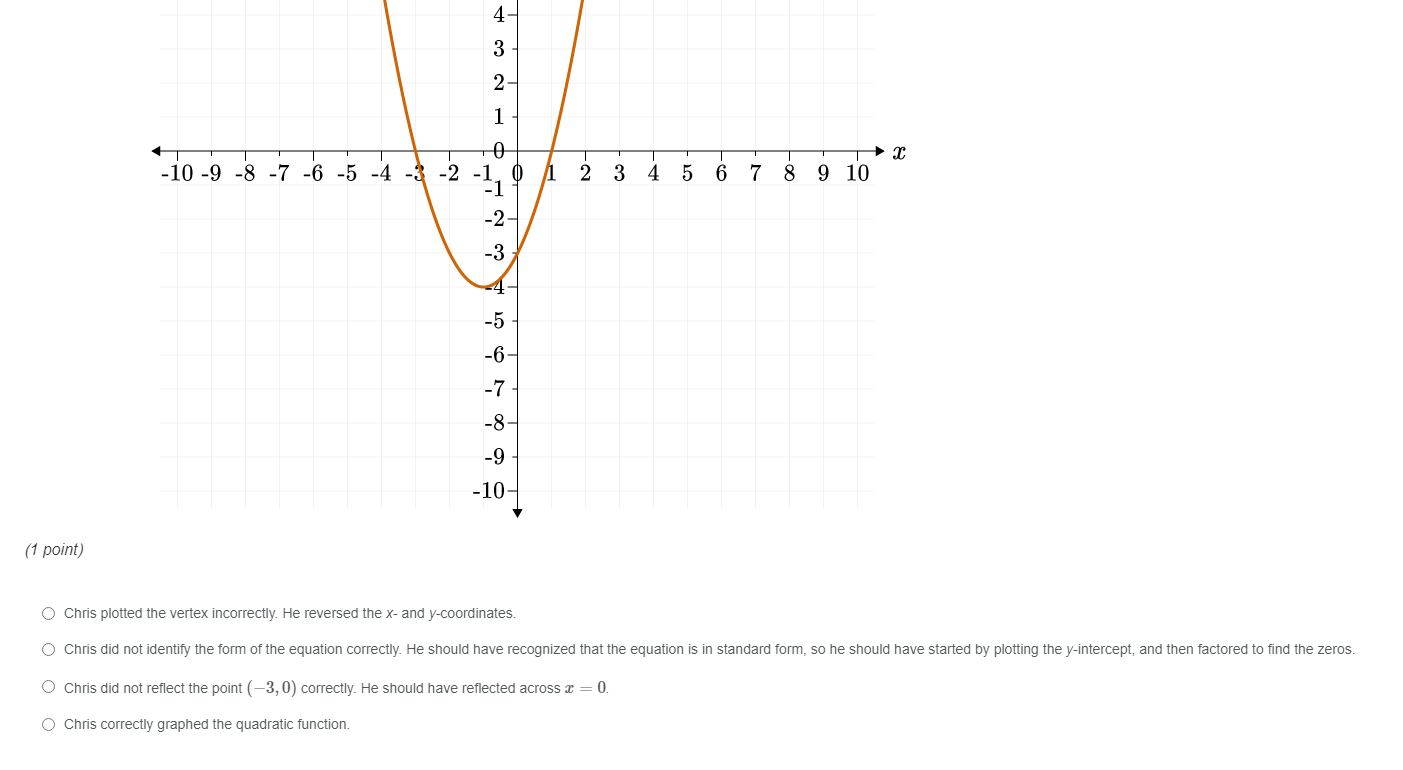
Solved Chris Is Asked To Graph The Quadratic Function F X Chegg Com

Example 4 Write A Quadratic Function In Vertex Form Write In Vertex Form Then Identify The Vertex X 2x 2 10x 22 Y Solution X 2x 2 10x 22 Y Write Ppt Download

How To Rewrite A Quadratic Function To Find Its Vertex And Sketch Its Graph Algebra Study Com

2

Graphing A Qudratic By Converting To Vertex Form Youtube

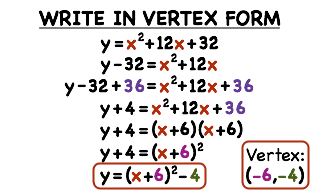
How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd

Characteristics Of Quadratic Functions

Mfg The Vertex Of A Parabola

Write The Equation In Vertex Form Y X 2 2x 8 Study Com

How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic

Ppt Converting Quadratic Equations Powerpoint Presentation Free Download Id

Finding Vertex Form Of A Quadratic Equation Learnmath

Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

1

Solved 5 Write The Equation Of The Parabola In Vertex Form Chegg Com

1

Y Classzone

What Would An Equation For A Quadratic Function In Vertex Form With Vertex 1 6 That Passes Through The Point 3 4 Be Quora

Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath

How To Graph Parabolas Krista King Math Online Math Tutor

How Do I Find The Vertex Of F X X 2 8x 7 Socratic

How To Graph A Quadratic Equation 10 Steps With Pictures

Ppt Ch8 Quadratic Equation Solving Methods Powerpoint Presentation Free Download Id

Find Factored Form And Vertex Of F X X 2 2x 8 Youtube

Standard Form To Vertex Form Definitions Facts And Solved Examples Cuemath

Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They

Complete The Square To Rewrite Y X2 8x 3 In Vertex Form And Then Identify The Minimum Y Value Brainly Com

Quadratic Functions

To Find The Vertex Transform The Quadratic Function From Standard Form To Vertex Form By Completing The Square Y 2x2 12x 10 2x2 6x 10 2x2 6x 9 18 10 2328 Square Meme On Awwmemes Com

2 1 Graphing Quadratic Functions Quadratics Exploration Patty

Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

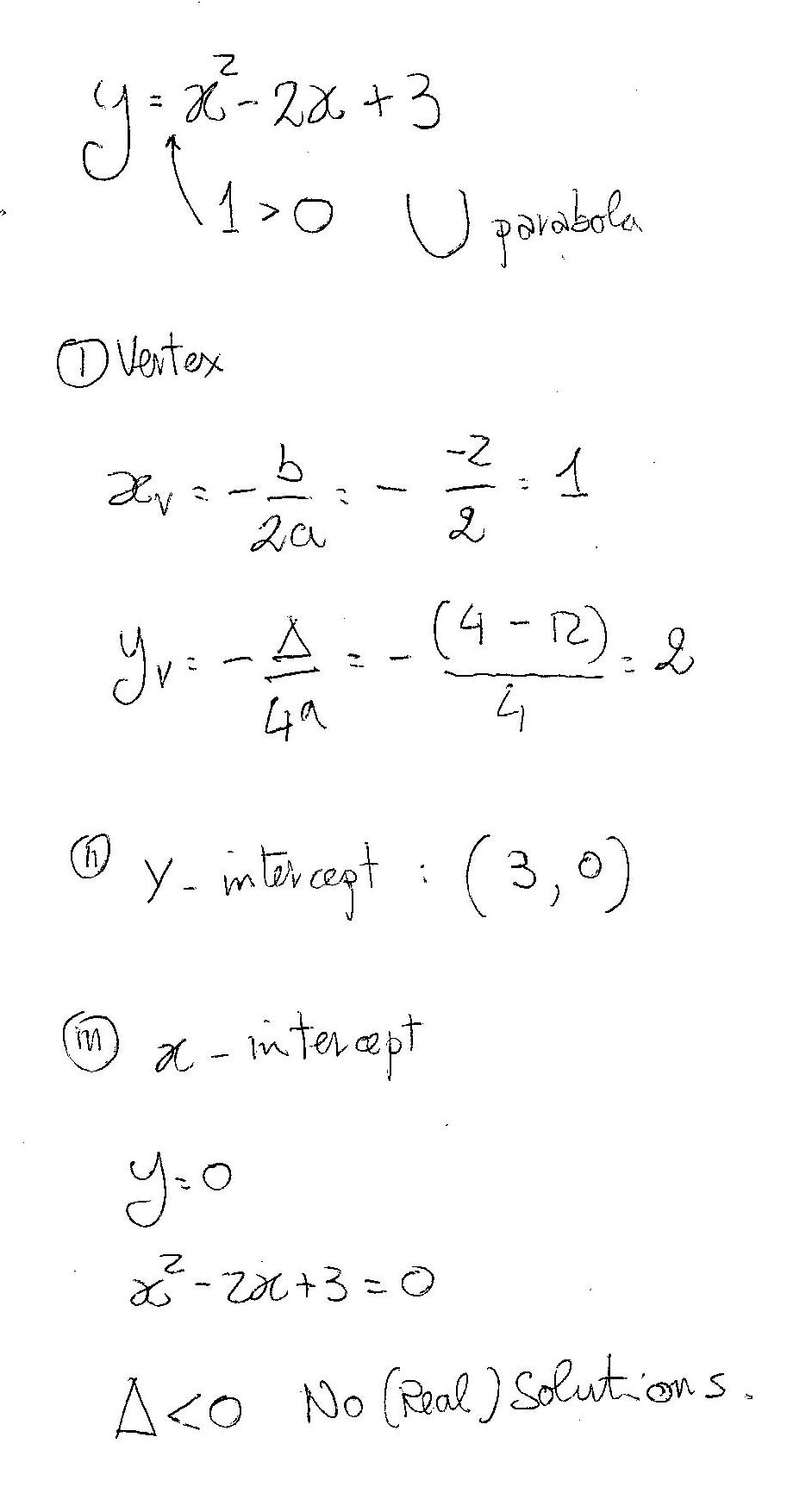
How Do You Graph Y X 2 2x 3 Socratic

Fireworks From Standard To Vertex Form Ppt Video Online Download

Quadratic Functions

Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mikes Calculators With Steps Free 21

2

1

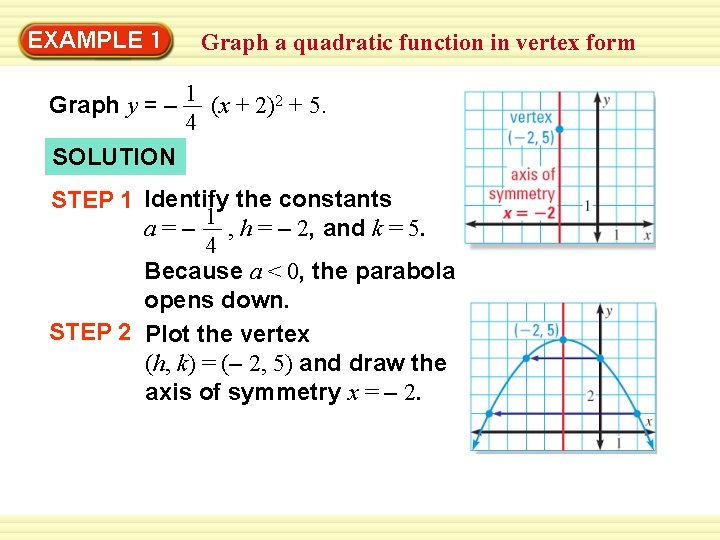
Vertex Form Of Quadratic Functions Math 2 Y

3

Which Equation Is Y X 3 2 X 4 2 Rewritten In Vertex Form Brainly Com

Solution Given The Quadratic Function F X 2x2 8x 11 Use Completing The Squares To Convert The Quadratic Function Into Vertex Form State The Vertex Find The X And Y Intercepts

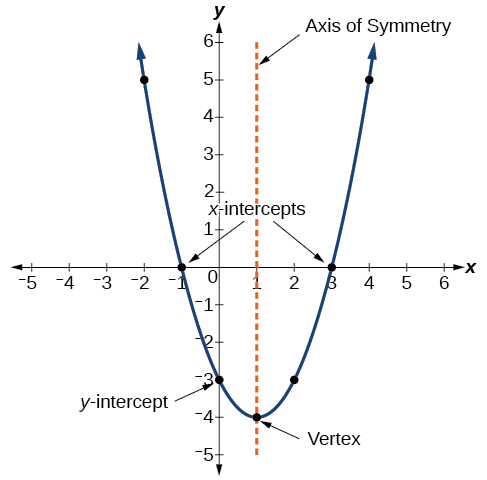
5 2 Quadratic Functions Mathematics Libretexts

Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora

4 2 Vertex And Intercept Form

2

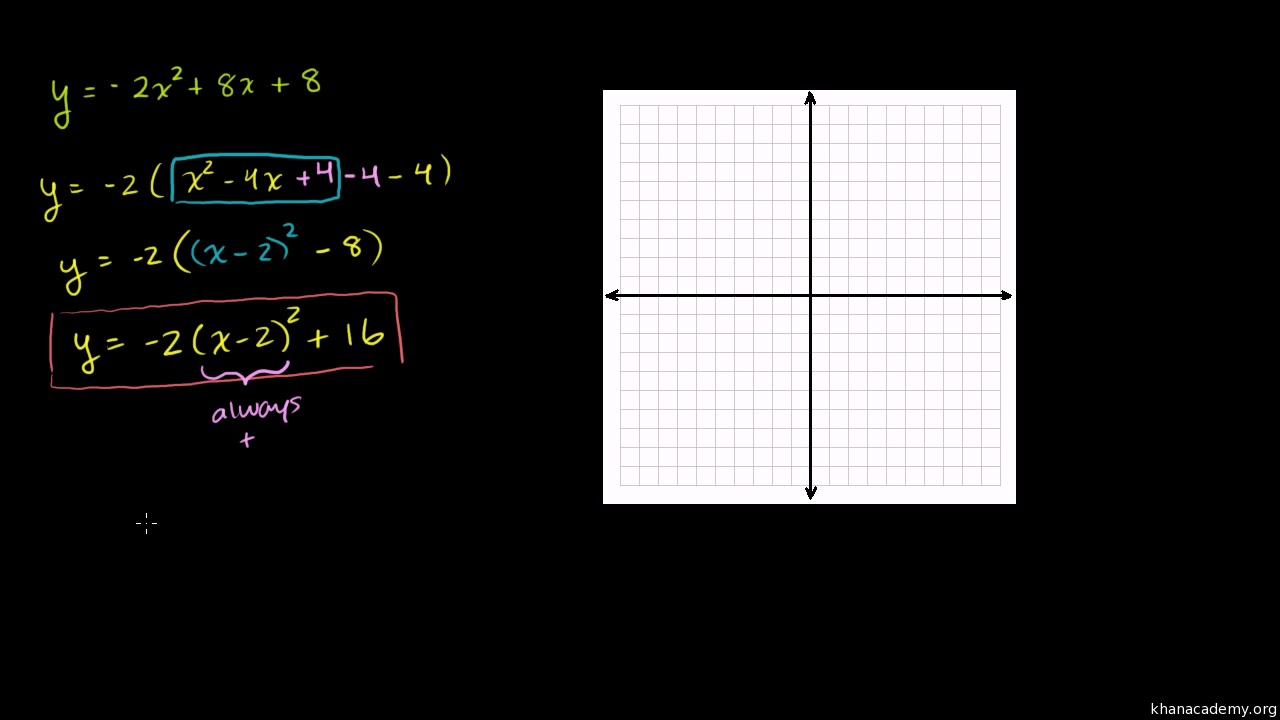
Vertex Axis Of Symmetry Of A Parabola Video Khan Academy

2

5 3 Vertex Form Of Quadratic Functions Translating

2

Solved Exercises 2 3 In Problems 1 8 Find The Vertex Form Of Chegg Com

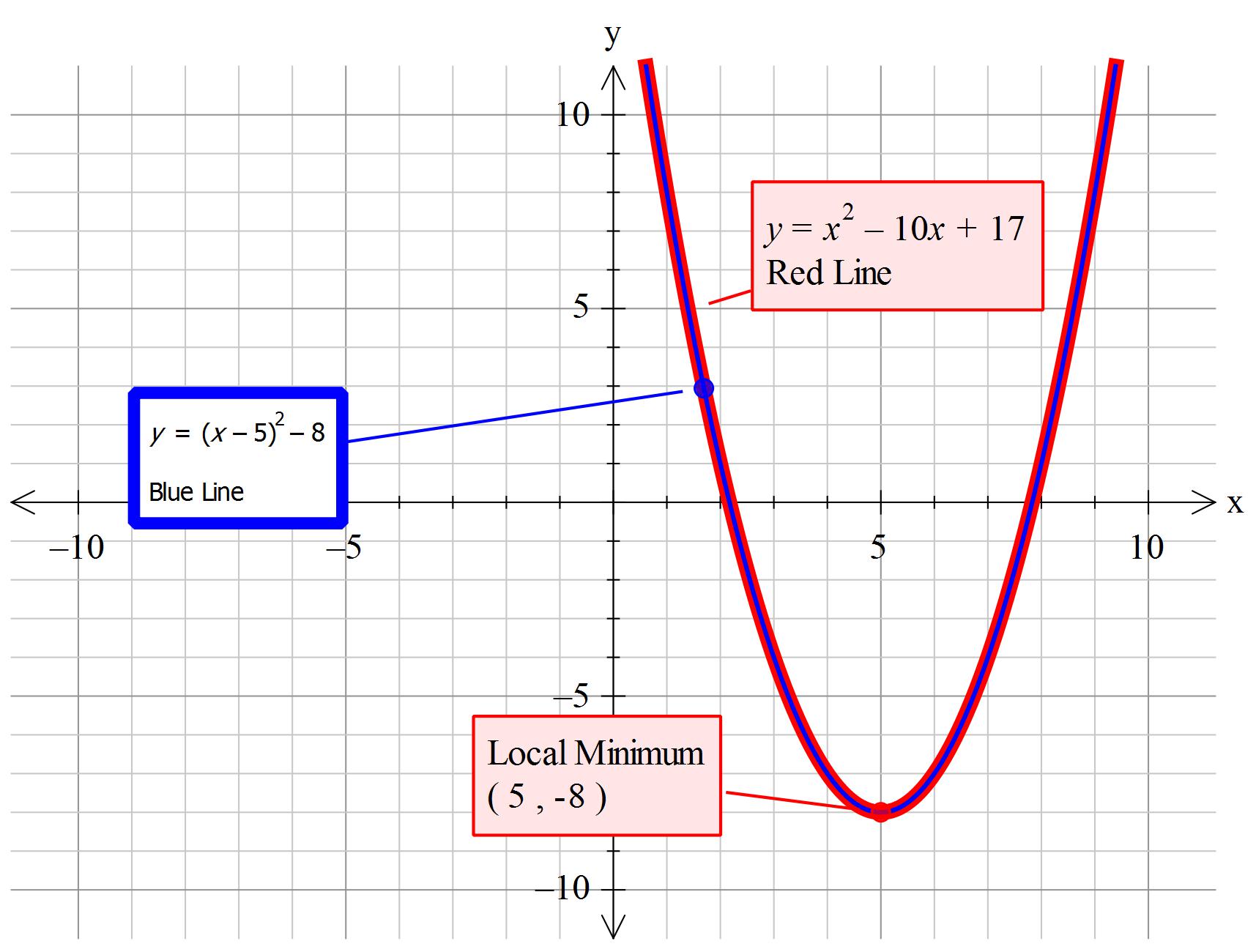
How Do You Write The Vertex Form Equation Of The Parabola Y X 2 10x 17 Socratic

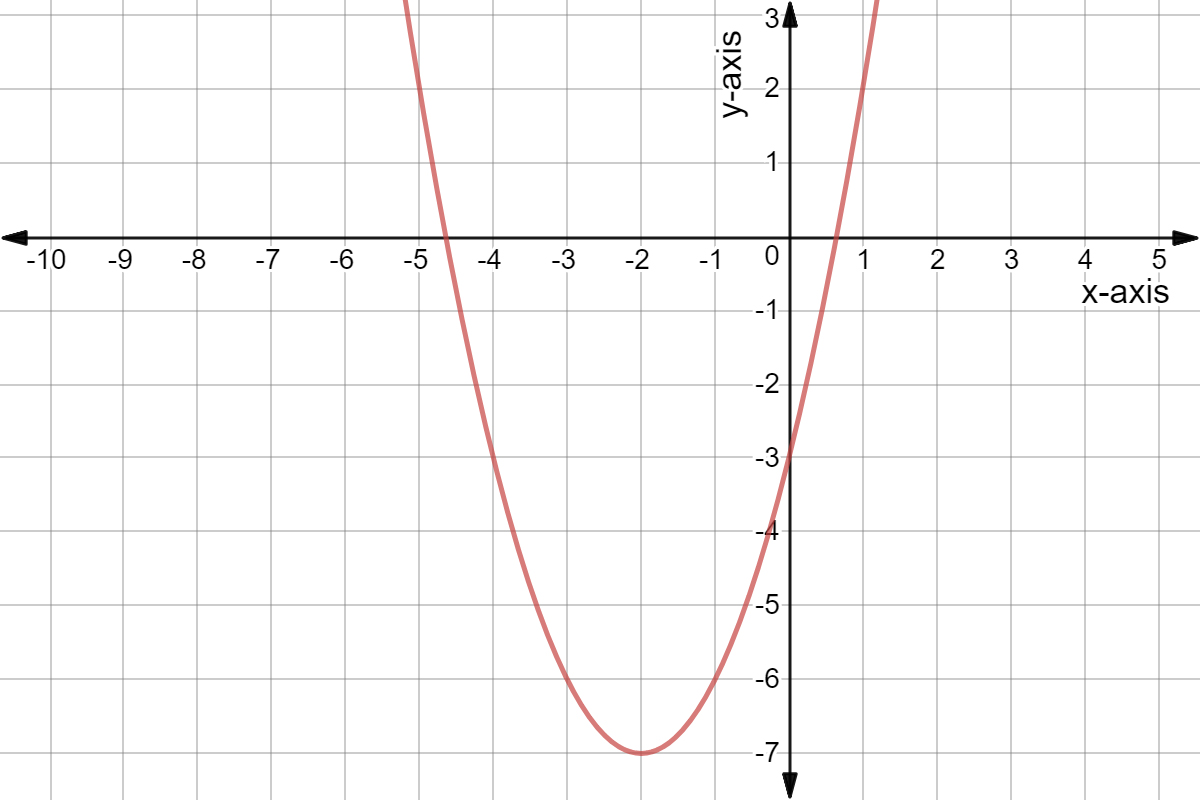
Completing The Square Vertex Form Of A Quadratic Expii

Solution What Is The Vertex Form Of F X X 2 2x 5

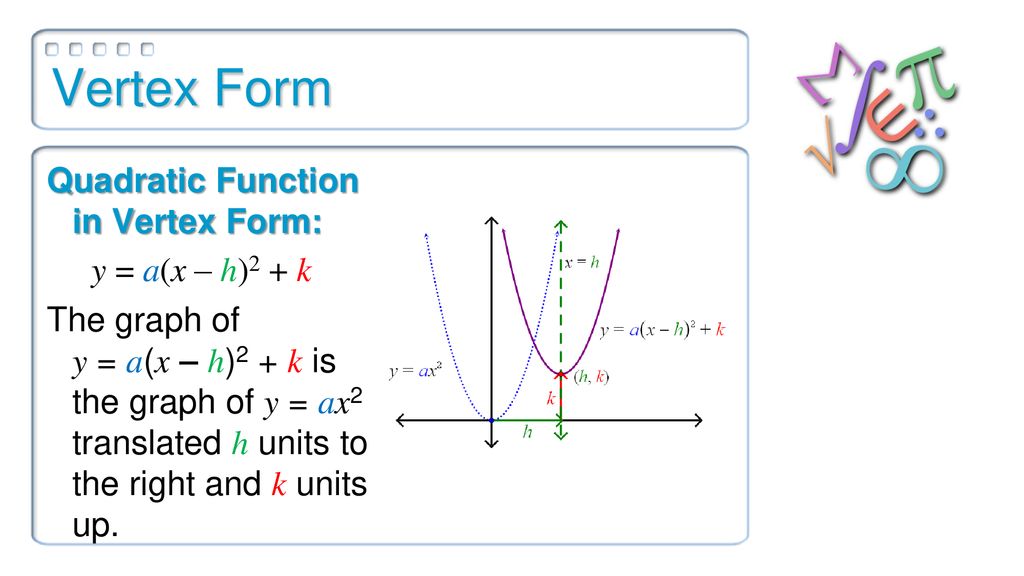
Vertex Form Quadratic Function In Vertex Form Ppt Download

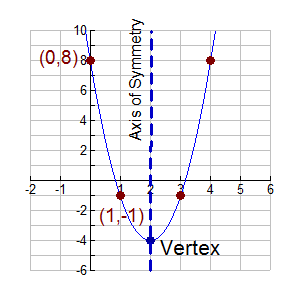
Vertex Form Of Quadratic Equation Mathbitsnotebook Ccss Math

Quadratics Review 1 Quadrtics Test Review 1

The Vertex Form Of The Function Is Choose The Equation That Shows A Step In The Process Of Brainly Com

1 Find The Vertex Point H K 2 A Will Be The A From The Standard Form Equation 3 Substitute Into Y A X H 2 K Ppt Download

Solved Question 5 Lt Put The Equation Y A 2x 8 Into The Form Y X H K Answer Course Hero

Wp Blogs Moundsparkacademy Org

Practice 1 2 Graphing In Vertex Form And Intercept Form

Changing Quadratic Functions From Standard Form To Vertex Form Flashcards Quizlet

Vertex Intercept And Standard Form Ck 12 Foundation

Graphing Quadratic Functions

Vertex Intercept And Standard Form Ck 12 Foundation

What S 27 In Vertex Form

2

7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download

Complete The Square Lesson Ppt Download